■ Group Study/Discussion : Project Topics
1) (Prof. Mahn Won Kim) Estimate the persistence length of the Freeway #1 between Seoul and Busan.
2) (Prof. Fyl Pincus & Prof. Mahn Won Kim) Measure the salting out concentration for NaCl in water, and compare it with a literature value, and an estimated value using a simple theory.
3) (Prof. Fyl Pincus) What would be the most stable configuration of a 2-dimensional polymer, whose contour is continuously charged, with its two ends being fixed in space? (When the two ends are fixed at the same spot, the answer should be a circle. But, when they are not in the same spot, it is not clear what it should be. The answer may not be a part of circle....
4) (Prof. Fyl Pincus) In dilute solution, the Debye length scales as c^(-1/2). Recently Perkin's group (Phys. Chem. Letters 2016) has observed using surface force balance experiments that at high salt concentrations (≥1 M) the screening length increases with salt concentration. Why might this be? (c is the concentration of 1-1 salt)
5) (Prof. Fyl Pincus) A flat solid surface has σionizable groups per unit area. The surface is covered by a layer of oil of thickness h. Outside the oil is water. In equilibrium what fraction of the groups ionize? How does this depend on h?
6) (Prof. Sarah Woodson) Consider a small RNA that can fold into a hairpin that is closed by a 5 bp hairpin. The loop of the hairpin can vary from 5 U's to 30 U's. The folding process can be decomposed into a nucleation step, which depends on the looping dynamics (related to the problem below), and "zippering" steps that describe the propagation of base pairs. Write a statistical model that described the folding pathway(s). Consider that the looping time depends on the loop size, chain stiffness, and excluded volume of the chain. Consider also that the base pairs are stabilized by interactions with the neighboring base pairs; these nearest neighbor interactions introduce a cooperativity to chain propagation. (For empirical energy parameters that describe this process, consult Freier et al. PNAS 1986 -- or one can try different assumptions about energy parameters.) Metal ions alter the chain stiffness -- how does this alter the predicted looping dynamics of the hairpin? (For experimental data describing such a system, see Kuznetzov, Nucleic Acids Res. 2007).
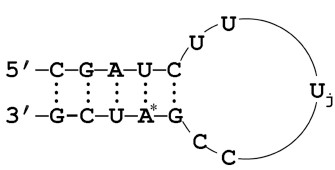
7) (Prof. Sarah Woodson) A slightly longer RNA contains two hairpins. The loops of the hairpins can interact. Estimate the overall Coulombic interaction interaction energy of the two RNA hairpins in water, assuming different degrees of charge neutralization by counterions. The entropic cost of counterion localization (from the bulk solution) can be estimated from RlnN. If the intrinsic energy of the loop-loop interaction is -10 kJ/mol at 25 ˚C, to what degree must the phostphate charge be reduced to allow the two hairpins to interact?
8) (Prof. Oleg Krichevsky) Consider ideal (no excluded volume interactions) and real polymers confined in a tube and/or stretched by an external force. What is the free energy cost /relevant forces of/for these deformations? What are the different confinement/extension regimes? Do the two situations (confinement and stretch) relate to each other?
9) (Prof. Oleg Krichevsky) Consider a long semi-flexible polymer (much larger than its persistence length) confined in a tube or stretched by an external force. Discuss different confinement and force-extension regimes.
10) (Prof. Omar Saleh) The ION EXCESS, Gamma, is a quantity that reports on the ions in solution surrounding a charged particle in a salt solution. It is defined, for, say, positive ions, as the difference between the number of positive ions surrounding the particle, and the number that would be there if the atmosphere had the uniform bulk salt concentration. You calculate this by the integral, over all solution surrounding the particle, of the difference between actual ion distribution, n(r), and the bulk concentration, n_0: Gamma = int d^3r ( n(r) -n_0)
You can calculate n(r) using certain models (e.g. Poisson-Boltzmann), and certain charged particle geometries, so you can calculate Gamma. The question is this: Take a spherical particle with charge Q smeared on the surface, and put it in a 1:1 salt solution. What is the ion excess per unit charge on the source, Gamma/Q, in the limit of very low salt concentration (n_0 ightarrow 0)?
11) (Prof. Alexandra Zidovska) Diffusion limited aggregation --- The rate of growth of a polymer depends on the speed with which monomers reach the polymer tip and the kinetics with which these monomers join the polymer. Thus the maximum speed that a polymer can grow in a cell is given by the rate that monomers reach the tip. If the monomers reach the polymer tip by diffusion in solution, this is called the diffusion-limited rate of growth.
Actin and microtubules are cytoskeletal filaments, whose polymerization drives essential cellular processes such as locomotion and chromosomal division, respectively. The concentration of actin monomer in cells is typically ~20 µM and the diameter of the polymerized actin filament is ~8 nm. A typical cellular concentration of tubulin is ~10 µM and the diameter of a microtubule is ~25 nm. Tubulin and actin monomers tend to have a diffusion coefficient, D, in cells of about ~ 5 µm^2/s.
(a) Assuming that the rate of growth of these polymers is diffusion limited (i.e. any monomer that bumps into the end of the polymer binds), use the diffusion equation to solve for the rate of growth of both types of polymer
(b) In each case, what is the monomer concentration profile away from the growing tip?
(c) The dynamics of individual microtubules can be measured in cells. This type of data reveals that a typical microtubule growth rate within a cell to be ~ 10 µm/min. How does this compare with the diffusion limited growth rate for microtubules?
12) (Prof. Changbong Hyeon) Consider the minimum-energy N point charge configurations on a 1) line with finite length (L), 2) circular disc (with radius R), 3) sphere.
13) (Prof. Rachel Segalman) A cross-linked polymer (e.g polyisoprene) with nc monomers per cross-link is contaminated with a homopolymer with n links per chain due to incomplete polymerization. The polymer is immersed in V ml of an extremely good solvent.
a) Will some of the homopolymer crawl out of the gel? Why?
b) Will there be a finite number of chains inside the gel at equilibrium? Why?
c) Will the size of the swollen gel and the concentration of homopolymer within the gel depend on V? Why?
d) In many applications, gels are washed several times to remove the homopolymer. Why is one washing sometimes not enough?
e) Indicate how you would derive the equations for obtaining the fraction of homopolymer chains inside the gel and the equilibrium size of the gel?
f) If you make a cube of polyisoprene homopolymer it will (within a few days) become a flat pancake (or a polymeric puddle). This is because polyisoprene is a liquid at room temperature and the chains are mobile. If you have a cross-linked polyisoprene that contains polyisoprene homopolymer, will the homopolymers crawl out of the cross-linked rubber to make a puddle around the cross-linked rubber? Hint: think of the quality of air as a solvent.

